Newtonovy fraktály

1 Newtonova metoda tečen

1.1 K čemu to je?

Newtonova metoda je jedním ze způsobů, jak numericky vypočítat rovnici typu f(x)=0, x je reálné číslo. Existují samozřejmě i jiné metody řešení takovýchto rovnic. Newtonova metoda velice rychle konverguje - viz 1.2, nevýhodou je, že když máme složitější funkci, musíme přibližně vědět, kde se kořen nachází - o tom je odstavec 1.3.

1.2 Popis metody

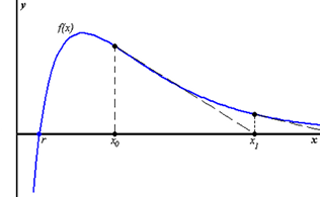
Jak funguje Newtonova metoda, je vidět na obrázku č.1.
1. Zvolíme počáteční bod x¹.
2. Vedeme z bodu o souřadnicích (x₁,f(x₁)) tečnu ke grafu funkce, a místo, kde se protne s osou x, označíme x₂.
3. Vedeme z bodu o souřadnicích (x₂,f(x₂)) tečnu ke grafu funkce, a místo, kde se protne s osou x, označíme x₃.
4 - n. Iterujeme do zblbnutí (matematici) nebo do požadované přesnosti (fyzici), až se dostaneme velice blízko ke kořenu funkce r.

Obrázek č.1: Newtonova metoda tečen

1.3 Nevýhody metody

Pokud neznáme přibližně, kde se kořen nachází a máme složitější funkci, je problém ke kořenu dokonvergovat z následujících důvodů:

• 1. Divergence směrem od kořenu, viz obrázek č.2. Na obrázku máme maximum, funkce je na levé straně od maxima rostoucí a protíná nulu. Na pravé straně od maxima je funkce klesající a jen konverguje k nule a nulu nikdy neprotíná. Když zvolíme počáteční bod NM na pravé straně od maxima, metoda nám nikdy nedokonverguje ke kořenu.
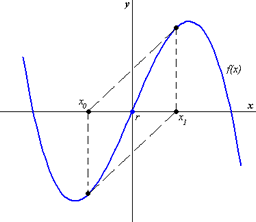
• 2. Nešťastně zvolíme počáteční bod v minimu nebo maximu funkce, viz obrázek č.3.
• 3. Metoda se zacyklí, viz obrázek č.4, to se stane, pokud je kořen funkce v inflexním bodu funkce.

2 Newtonovy fraktály

Newtonův fraktál vznikne, pokud necháme konvergovat komplexní funkci pomocí Newtonovy metody s počátečním číslem z komplexní roviny ke kořenu funkce. Fraktál se utvoří díky nevýhodám Newtonovy metody, a to kvůli nevýhodě č.1. Část počátečních bodů nedokonverguje a část dokonverguje. Když vyneseme počáteční body, které dokonvergovaly, do grafu (komplexní roviny), vytvoří se nám fraktální obrazce.

3 Jak jsem generoval a barvil fraktály

Já jsem své fraktály generoval v programovacím jazyce pro děti PASCALU, obarvil jsem modrou barvou oblast nejrychlejší konvergence postupně přes červenou, přes světlé barvy, až k tmavým barvám - oblast nejpomalejší konvergence (postupně standardní barvy v Pascalu 1 až 128). Barevná škála je vidět na obrázku šnek 1 - na okraji šneku modrá funkce konverguje nejrychleji, až uprostřed šneku funkce konverguje po více než 128krocích k výsledku s danou přesností. Zajímavostí je, že generování fraktálu o rozlišení 2048*1536 trvalo na počítači o výkonu 2GHz (procesor Intel), pamětmi DDR2 asi 30minut.

4 Klasické Newtonovy fraktály

Jen na ukázku (tohle umí každý).

f(z)=z³-1

f(z)=z⁹-1

3 Newtonův Fraktál s komplexním kořenem

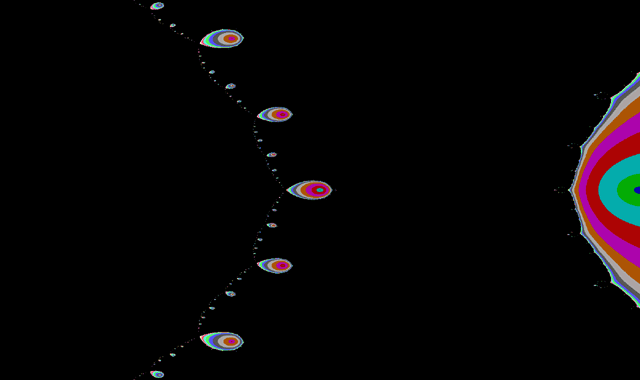
Trochu zajímavější. Každý přívěsek řetízku je bod konvergence. Je zde zas nekonečně mnoho přívěsků na řetízku. Každý přívěsek má na sobě další řetízky spojené do kruhu a takto se fraktál opakuje.

f(z)=(z+0.5i)(z-0.5i)(z-1)

4 Newtonův fraktál s komplexní mocninou

f(x) = z⁴ⁱ-1

Zde jsou ohromně zajímavá centra nejvzdálenější konvergence, vždy ve středu šneka (spirály).

Celá komplexní rovina - střed obrazovky je počátek souřadnic.


Šnek 1 - vybraná část z "celé komplexní roviny"



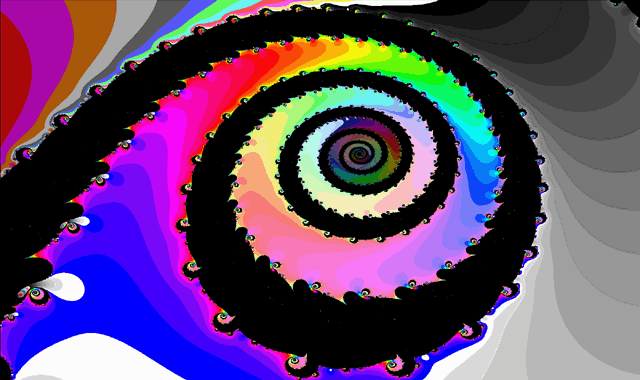
Šnek 2 - vybraná část z obrázku Šnek 1



Šnek 3- Vybraná část z obrázku Šnek 2



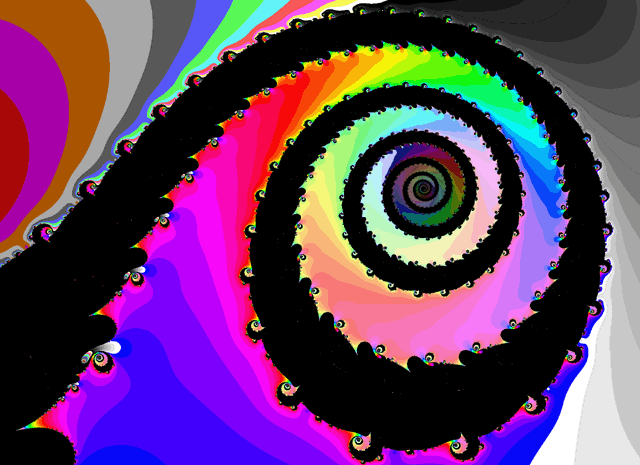
Zvětšenina jedné z malých teček (asi 1 pixel) na obrázku celé komplexní roviny

---

[1] obrázek č.1 jsem převzal z: http://faculty.wlc.edu/buelow/calc/nt4-8.html
[2] obrázky č.2, 3, 4 jsem převzal z: http://en.wikiversity.org/wiki/Newton's_Method